0.9999999… (with an infinite amount of 9) equals 1.
Doubting ? Here is the mathematical proof:
1/3 = 0.333333...
Statement A: 3 x (1/3) = 3 x 0.333333...
Statement B: 3 x (1/3) = 1
A implies 3 x 0.333333... = 0.999999...
A = B implies 0.999999... = 1
2 = 4.
Other mathematical proofs can be found in the commentaries on the french version of this DYK.
In order to preserve the team's health, we advise you to take a look on the french version of this DYK and its (numerous) comments.
I knew that since I was 13
this proof given isn't very good, as all would need argued is 1/3 simply cant be truly expressed in decimal form and 0.3333~ is just the closest interpretation… the proof i tend to use is:
.999999~ * 10=9.999999~
9.9999~ – .9999999~ = 9 (truncating the decimals off)
however none of these proofs are truly proof, cause one could argue that 9.9999999~ represents 9.999~ – 0.00000~9(IE 1 decimal place shy of infinity)
however it should just be accepted as true, because there are no 'ways' to get .3333333~(aside from assuming 1/3 actually does equal it, or starting with it, or another repeating decimal)... there is no harm in using it, but to some (including computers), it makes things easier…
I've ran through at-least 20 different 'proofs', seeing the logic behind them none actually convincing me anything beyond accept it because it doesn't 'break' Our math..
this proof given isn’t very good
Indeed : the point was to have something “easy to read”. A nicer proof would be “if the two numbers weren't the same number, there should exist one given number separating them”.
Or this “trivial when you have learnt limits” :
0. 99999999… = Lim (x—>+oo) 1 – 1/(10^x) = 1
(and your maths teacher would have beaten you up when you have written Lim (whatever) ~ = (something) : Limit equals )
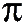
This is not true…think about it. If there is an infinite number of 9s, that means that the string of 9s goes on forever – and though we can round it up for theoretical purposes it is not a literally equality.